bayesian statistics Archives

Several weeks ago I wrote a post on Bayesian statistics. I was very interested in the implementation of Bayesian statistics, especially for complex problems which are more easily solved with simulation rather than mathematical manipulation. I wrote the article with a specific audience in mind: namely those that knew the basics of Bayesian statistics, but had no idea how to implement it. That probably confounded the issue.

As an astute commenter pointed out, in my excitement to implement my Bayesian program, I skimmed over several key points of Bayesian statistics and woefully mis-represented others. Let’s fix that now, shall we! Let’s talk about the basics of Bayesian statistics, and then move up to simulating them.

Bayes’ Theorem

Derivation

If I hand you a six-sided die, what is the chance that you’d roll a three? Hopefully you answered $\frac{1}{6}$ ! What is the chance that you’d roll two threes in a row? $\frac{1}{6}\cdot\frac{1}{6} =\frac{1}{36}$ . We can generalize this:

$P(A, B) = P(A) \cdot P(B)$

This is true if and only if A and B are independent (in the example of the die). If A and B are dependent, that is, if the probability of one depends on the other, we can write the probability of both occuring as:

$P(A, B) = P(A) \cdot P(B|A)$

where $P(B|A)$ is the probability of $B$ given that $A$ has occurred. We can also rearrange it the other way ’round:

$P(A, B) = P(B) \cdot P(A|B)$

There is no difference in which probability we choose “first” because they both equal the same thing: the probability of both $A$ and $B$ . In fact, let’s set them equal to each other now:

$P(A) \cdot P(B|A) = P(B) \cdot P(A|B)$

Dividing both sides by $P(A)$ gives:

$P(B|A) = \frac{P(B) \cdot P(A|B)}{P(A)}$

BOOM! We call this equality Bayes’ Theorem. It’s super nifty: if we know something about $P(A|B)$ (e.g. the probability of getting lung cancer if you’re a smoker), we have a way to flip that around and find $P(B|A)$ (e.g. the probability you’re a smoker given that you were diagnosed with lung cancer.1🙁)

Naming conventions

Bayesians sure use a lot of lingo! Fortunately, everything stems from Bayes’ Theorem. There are four “parts” to the theorem, and each “part” has its own name and importance.

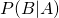$P(B|A)$ is called the posterior. It’s the thing we want to calculate.
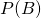$P(B)$ is called the prior or prior probability. It’s something we know (or assume) about the distribution of $B$ knowing nothing about $A$ . Bayesians take care in choosing their priors, because they can dramatically affect the calculation of the posterior.
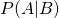$P(A|B)$ is called the likelihood function. This is the fantastic part of the equation that glues everything together. This is what links 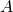$A$ up to $B$ .
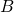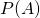$P(A)$ is called the marginal likelihood. Honestly, we don’t care about it much. It’s used to normalize the function so all the probabilities added together equal one.

Plainly spoken

Bayesians update their hypotheses as they go. This is why simulations can be useful in Bayesian statistics: it’s easy to propagate evidence through a simulation. It can be gnarly to do that analytically (with mathematical equations).

When predicting a hypothesis based on evidence, Bayesians use prior knowledge (usually an informed guess) in addition to the evidence. Frequentists use only the evidence. In situations where we understand the system (the coast guard trying to perform rescue operations and knowing the weather, previous rescue locations, and last-known coordinates) Bayesian statistics is a better method. In situations where you know little about the system, (“what happens if…?”) Bayesian statistics can perform poorly because you may not consider certain outcomes based on the original bad guess.

Some examples

The infinite cookie jars

I present you with two cookie jars.

A cookie jar with two elephants. The jar is turquoise and blue and has two handles.

A cookie jar with a happy panda. The panda is covered in crumbs. The jar is a light green color.

They are both magical cookie jars. You reach your hand in, and a cookie materializes in it. You can have infinite cookies! These jars are the best thing ever. Aren’t you happy?! Jar one has a 50% chance to give you chocolate chip cookies and a 50% chance to give you peanut butter.2 Jar two is 75% chocolate, 25% peanut butter.

I’m being really nice here, and have offered you one of the cookie jars for keeps. I forgot which one is which, so… sorry about that.

You pick a jar. What is the probability you picked jar one? Well, right now it’s 50%. There were two jars, and you picked one. And I bet you’re craving a cookie, so you pull one out. It’s chocolate chip. What’s the new probability you picked jar one?

After picking one cookie

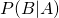$P(B|A)$ , the posterior, what we want to calculate: what is the probability of jar one given that you pulled3and are consuming4if you don’t want it, I’ll eat it a chocolate chip cookie.
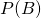$P(B)$ , the prior: what was the probability you grabbed jar one before you pulled out a cookie? (50%)
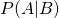$P(A|B)$ , the likelihood function: what is the probability of drawing a chocolate chip cookie if you’re holding jar one? (50%)
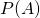, the marginal likelihood: what was the (overall) probability of drawing a chocolate chip cookie? This is the probability of chocolate chip from each jar times the probability of holding that jar:
- $P(CC|J1)\cdotP(J1) + P(CC|J2)\cdotP(J2)$
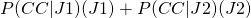
- = (0.5)(0.5) + (0.75)(0.5)
- = 0.25 + 0.375
- = 0.625
- (You were 62.5% likely to get a chocolate chip cookie no matter what.)

Putting it all together:

$P(B|A) = \frac{ P(B) \cdot P(A|B) }{ P(A) } = \frac{0.5 \cdot 0.5}{0.625} = 0.4$

There’s a 40% chance you’re holding jar 1. Neat, huh? Let’s pull another cookie and see what happens! You draw it out and… another chocolate chip.5

After picking two cookies

Our prior changed; instead of $P(B)$ = 0.5 it now is 0.4. The marginal likelihood changed as well! $P(A) =P(CC|J1)\cdotP(J1) + P(CC|J2)\cdotP(J2)$
$= (0.5)(0.4) + (0.75)(0.6) = 0.65$

What does this mean for the probability of holding jar 1?

$P(B|A) = \frac{P(B) \cdot P(A|B)}{P(A)} = \frac{0.4 \cdot 0.5}{0.65} = \frac{4}{13} \approx 0.31$

Three cookies?

The third cookie you draw is also chocolate chip! Holy smokes! The new probability of grabbing a chocolate chip cookie: $P(A) =P(CC|J1)\cdotP(J1) + P(CC|J2)\cdotP(J2) = (0.5)(0.31) + (0.75)(0.69) = 0.67$

And the new probability of holding jar 1:

$P(B|A) = \frac{P(B) \cdot P(A|B)}{P(A)} = \frac{0.31 \cdot 0.5}{0.67} = \frac{8}{35} \approx 0.23$

There’s still about a one in four chance you have jar 1, but more likely than not, you have jar two. I hope you like chocolate chip!

Lung Cancer

You’re probably aware that smoking cigarettes gifts you an increased likelihood of developing lung cancer. You may even be aware of what that likelihood is. But how was this likelihood calculated?

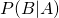$P(B|A)$ : What is the likelihood of getting lung cancer, given that you smoke?
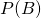$P(B)$ : Assuming no information about smoking, what is the probability of getting lung cancer. According to cancer.org, it’s 1 in 14 for men and 1 in 17 for women; let’s call that 0.065.
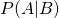$P(A|B)$ : What is the probability of being a smoker, given that someone has lung cancer? This is easy to gather6: ask all of your lung cancer patients if they smoke. The CDC links smoking and lung cancer in 80% to 90% of cases. Let’s call that 0.85.
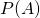$P(A)$ : What is your probability of being a smoker? Again, according to the CDC, in 2015 roughly 15.1% of adults smoked.7

$P(B|A) = \frac{P(B) \cdot P(A|B)}{P(A)} = \frac{0.065 \cdot 0.85}{0.151} \approx 0.37$

Simply by adding information about a person’s smoking, their chances of getting lung cancer went up from ~6.5% to ~37%. This number is larger than reported literature (I found numbers ranging from 13% to 25%), but there were some significant limitations of my model, so I’m not too worried.8

What about the probability of getting lung cancer assuming you’re a non-smoker? (Here we use $A$ to mean “non-smoker.”)

$P(B|A) = \frac{P(B) \cdot P(A|B)}{P(A)} = \frac{0.065 \cdot (1-0.85)}{(1-0.151)} \approx 0.01$

Jumping Jimminy! According to this model, non-smokers only have about a 1% chance of getting lung cancer.9

In Conclusion

You can definitely use Bayesian statistics on problems that don’t require simulations. As long as you’re using Bayes’ theorem, you’re doing Bayesian statistics. My last article was great if you want to jump-start into the simulation world, but it’s clearly important to understand the fundamentals first. I hope this helps!