entropy Archives – RealThinks

I have been down with the flu for… gosh, it feels like two weeks now. Not fun.

I’ll spare you the gory details, but as I’ve been floating around my home in a haze of flu-induced bleh, I am constantly reminded of how much I’ve fallen in love with the nasal rinse as one of my go-to sickness helpers. If you asked me two years ago about nasal rinses, I would’ve said, “no way never nope not going to happen.” You, gentle reader, may also be in this boat. Maybe you had the same misconception I had: that this would hurt.

Thinking about purposefully pouring water up your nose, at least for me, is reminiscent of the days when Dad made you laugh at the dinner table and you snorted out milk… ow. Accidentally get water in your nose from the pool or shower? OW. Nasal rinses don’t hurt, and the reason why has to do with osmotic pressure.

What is osmotic pressure? Well, let’s back up a little bit and first talk about the concept of entropy. I get a little irked at people who describe entropy as “chaos.” It kind of is, I guess. But that dramatically over-simplifies things and leads to a lot of misunderstandings (“how can anything ever be ordered if the natural state of the universe is chaos?”). “Chaos” also sounds really unappealing, where entropy, when properly understood, is quite a beautiful, symmetrical, thing.

Let’s start with an example. Say you have this box, with two different kinds of gas on either side, separated by a barrier:

A rectangular box with a solid line drawn down the center. There are 12 red spheres on the left and 12 blue spheres on the right.

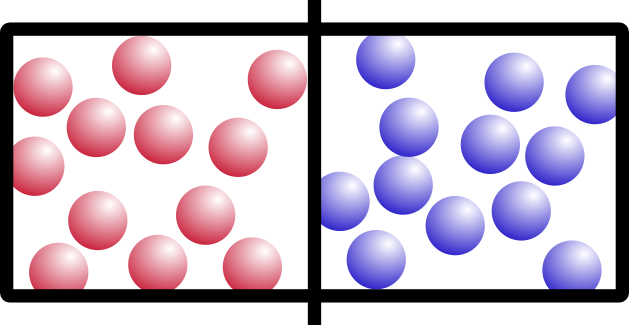
I’m going to call them “red” gas and “blue” gas. Because I can.

So what happens if we remove the barrier? Think about it for a minute. It’s not a trick question. Which of these would happen:

Three boxes similar to the one above are pictured, but with the center barrier almost entirely removed. In graphic A the red balls are on the left and blue balls are on the right. In graphic B, the balls are evenly intermixed. In graphic C, the blue balls are now on the left and the red balls are on the right.

If you said B, you’re right. Entropy is a movement of the system toward everything being more spread out and equal. This appeals to my sense of symmetry in the universe, and hopefully it appeals to yours too.

Entropy is also temperature dependent. Let’s try the same example, but say we have two solids on either side of the chamber. Think of them like ice in a freezer:

The same box as before is pictured, with the barrier fully lowered. On the left is a tightly-packed pyramid of red balls. On the right is an equally-packed pyramid of blue balls.

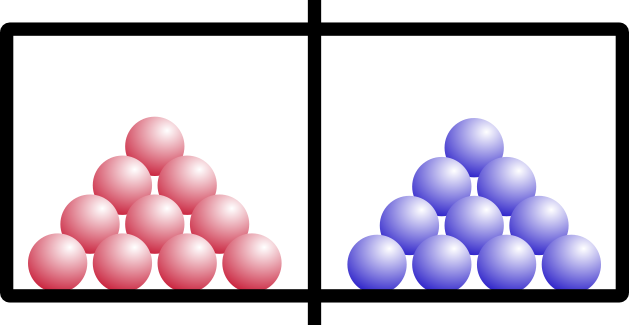
“Red” ice and “blue” ice, amIright?

So what happens if we open the barrier? Remember that these are solids, like your keyboard or emergency coloring book (everybody has one of those, right?).

Three choices are shown. The barrier is removed in all three. Graphic A shows the pyramids in the same place: red on the left, blue on the right. Graphic B shows the two pyramids with some of the balls swapped so that both pyramids are a mixture of colors. Graphic C shows the blue balls now on the left with the red balls on the right.

If you said A, you’re right. Solids don’t have enough energy to mix around… they would if they could (entropy), but they’re just too stuck-together for that to happen. You can imagine adding heat to our ice (after all, heat is a form of energy)… as soon as our blocks melt, the liquids will mix together, exactly as you would expect.

Speaking of liquids, I think we have enough in our toolkit to talk about… OSMOTIC PRESSURE (dun Dun DUN). Osmotic pressure discussions are often drawn with a U-shaped contraption for various reasons, but I’m going to mostly stick with the box diagrams for clarity’s sake. Let’s change a few features of the box, one by one. First, we’ll fill the whole box with water, and our balls are now salt (or “ions” if you want to be super fancy):

The original box: barrier in place, red balls floating on the left, blue on the right. A light turquoise background now fills the box.

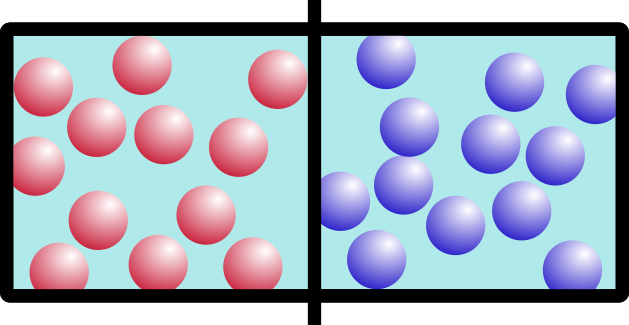
With me so far? Now, let’s cut little cheese-holes in the barrier so that water can get through it, but not our big, bulky salt/ion molecules.

The graphic is as before: red and blue balls floating in water, separated from each other by a barrier. The barrier, however, is now represented by a dashed line.

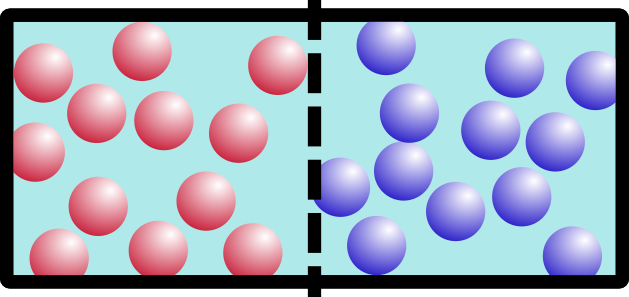
This sort of barrier is permeable (passable) by water, but not by ions. Dare I say it’s even… semi-permeable. Semi-permeable membranes appear all sorts of places. They’re in the grocery store contraption that gives you filtered water. Relevant to our discussion today: almost everything in YOU is a semi-permeable membrane. Your blood vessels are semi-permeable. The mucus membranes in your nose are semi-permeable. The awesome layer around your brain that only lets really important things through… you guessed it, is semi-permeable. Let’s file this information away in our back pocket and bring it back in just a bit.

Alrighty, alrighty. One last change to our box before the magic happens. We’re going to make the left-most and right-most sides of the box movable. Effectively, the volume on each side of the box can change. Maybe it would be helpful to think of the top and bottom of the box as elastic bands; the sides can sloosh back and forth like a slinky. Make sure you can properly conceptualize this, because it gets important very quickly:

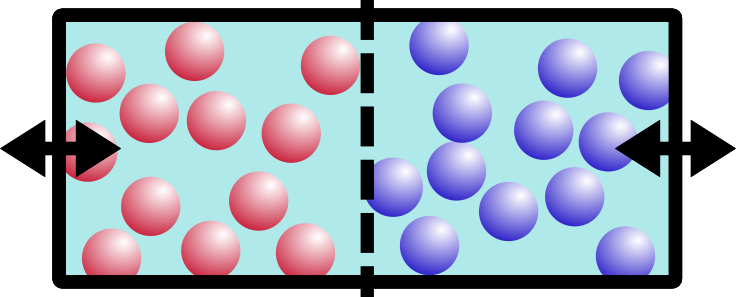
The box is now shown with double-ended arrows on the left and right side, indicating that the walls of the box can move freely.

Our picture so far should behave just like our boxes from before. Now! Are you ready for the magic change?! We’re going to wave our magic wand and *poof* disappear all of the ions/salt from one side of the box. POOF:

All of the blue balls have been removed from the right side of the box. Now only red balls remain, and only on the left.

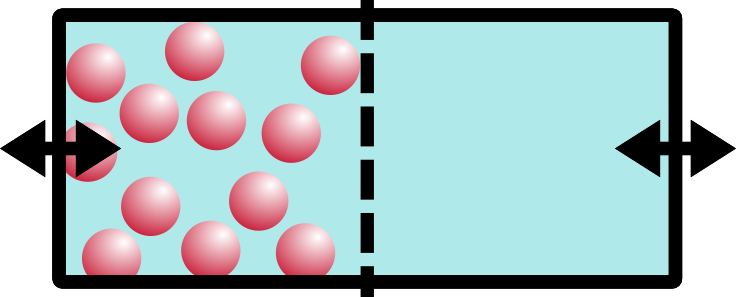
poof

Aaaah! Oh no!! Things are NOT even. Not even at all!! Entropy simply will not have this. So what does the system do to compensate? Entropy will drive the system walls to shift, moving water over from the empty side to the salt-concentrated side. The concentration of the system will balance out. Entropy has made things even, yet again!!

The walls of the box have both shifted to the left. The semi-permeable membrane is now on the right-most edge of the box, and the red particles are arranged evenly throughout the new space. The old box position is outlined in a light dashed line, showing the extent of travel.

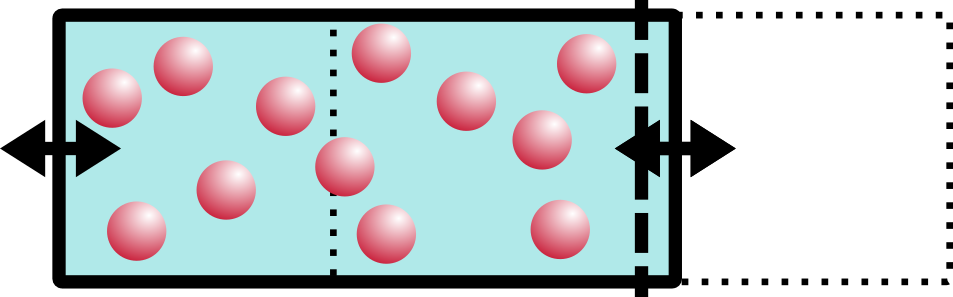
I imagine the water going “slooosh” as it shifts from the right side to the left.

That’s osmotic pressure in a nutshell. “But wait!” the astute observer might notice, “you didn’t say anything about pressure at all!” You are absolutely right, dear reader. There is an almost-linear relationship between pressure and volume everywhere you look. If you increase the pressure inside of a balloon, say, the volume will also increase. By pushing water into the left side of the box, we increased the volume and thus also increased the pressure. BOOM. Osmotic pressure. Maybe the U-diagram will make a little more sense now, too.

A tube shaped like the letter U is shown. At the top left of the tube is a grey rectangle labelled "pressure sensor." A semi-permeable membrane is indicated with a dashed line at the bottom center of the U. The left side of the tube has red balls in it, the right side has none. Arrows indicate the flow of water: the right side has an arrow pointing downward and less water; the left side has more water and an arrow pointing up.

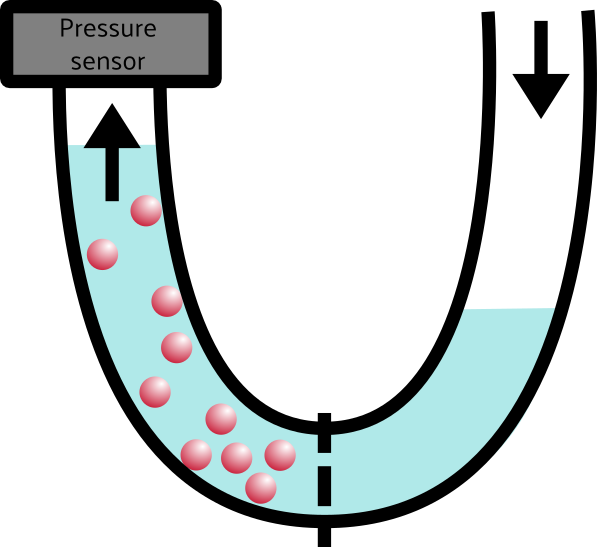
As water flows from the low-concentration (right) side of the tube to the high-concentration(left) side of the tube, the pressure on that side increases, which we can measure with the pressure sensor.

Wow! What a long-winded post. I hope you’re all sticking with me so far! Because I’m about to tie this up in a tidy bow. Your nasal mucus membranes are semi-permeable membranes. Your body is also naturally salty (What do boogers taste like, amIright? *backs out of room slowly*). If you put water in your nose, it will disrupt that delicate salty balance and your nose will actually ABSORB the water to try to balance it out. OW! Water in your eye?! Ow! Too much water into your blood vessels? Dead!

But what if we use a water solution that has the exact same salt content as your body? Water will be flowing neither in or out. It feels natural. This is what gives us nasal rinse, eye drops, and saline (aka “salt”) IV bags. We call these exactly-right salt concentrations isotonic. Iso = equal, right? And if you know a smidge of Latin, I bet you can guess what hypotonic and hypertonic are. (Spoiler: lower concentration and higher concentration than body salt, respectively.)

With the proper isotonic nasal rinse solution, flushing out my nose has never felt cleaner and more refreshing. You’re welcome for that detail. Now rinse away, happy readers, and revel in the beauty of breathing through your nose because I am going back to bed.